RFC: The mathematics remainder operator is incorrect?, it is a modulo operator

1

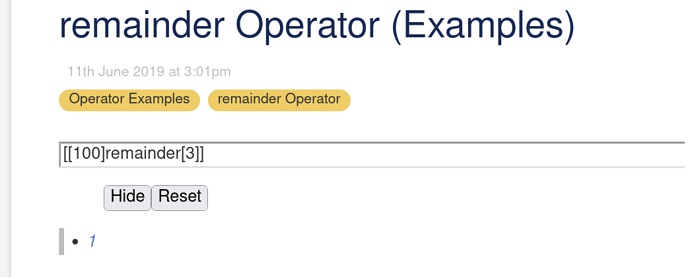
Place the following code in a tiddler on tiddlywiki.com to see “The mathematics remainder operator is incorrect, it is a modulo operator”

  • We also do not have the complement to the correct remainder operator the simple integer or int.

[Edited] The above .remainder operator needs work to cope with numbers that may not contain a period, ie whole numbers.

\function .int() [split[.]first[]]
\function .remainder() [split[.]last[]addprefix[.]]
\function .modulo(a)  [divide<b>.remainder[]multiply<b>round[]]
\procedure analysis(a b)
;For a=<<a>>, b=<<b>>
# a divide b {{{ [<a>divide<b>] }}}
## Ceil {{{ [<a>divide<b>ceil[]] }}}
## .Int {{{ [<a>divide<b>.int[]] }}}
## .remainder {{{ [<a>divide<b>.remainder[]] }}}
# a remainder b {{{ [<a>remainder<b>] }}}
## a modulo b {{{ [<a>.modulo<b>] }}}
\end

<<analysis 100 3>>
<<analysis 100 6>>
  • Further see my custom operators with a leading . for comparison.

Questions

  • Is my assertion correct?
  • what if anything can we do to fix this?
  • How do we maintain backward compatibility with an error?
  • Shall we make/fix the int/remainder operators?
2

I do not see the problem. Modulo - Wikipedia

The TW examples work for me.

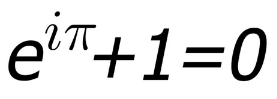
image
image1045×424 27.1 KB

3

Remainder behaves as if its modulo, in my example see how I arrive at the modulo.

  • Proving to me tiddlywikis remainder operator returns the modulo supports my argument.

The remainer I am familiar with is what remains after the decimal when a division is imperfect. eg 100/3 = 33.333333333 or .33333333 is the remainder, this is what we get when we use a calculator, an integer and a remainder.

Here I ask ChatGPT ;

In mathematics what do we consider the remainder?

In mathematics, the term “remainder” typically refers to the amount left over after performing a division operation where the divisor does not exactly divide the dividend. More formally, when a dividend ( a ) is divided by a divisor ( b ), the division results in a quotient ( q ) and possibly a remainder ( r ). This relationship is described by the equation:

[ a = b \times q + r ]

Here:

  • ( a ) is the dividend (the number being divided).
  • ( b ) is the divisor (the number by which the dividend is divided).
  • ( q ) is the quotient (the result of the division).
  • ( r ) is the remainder (what’s left over after the division).

The remainder is always less than the divisor and can be zero if ( a ) is exactly divisible by ( b ). In many mathematical contexts, especially in modular arithmetic, the concept of the remainder is fundamental. For example, when working with clock arithmetic (a type of modular arithmetic), the remainder determines the position of the hands on the clock.

Specifically is says;

In computer science, the remainder operation is often implemented as the modulo operation, which provides the remainder of a division between two numbers.

So our remainder operator is from computer science and not everyday mathematics.

4

I’ve never seen the term remainder used to describe .33333. That is what I would call the fractional part of the number.

From the equation you shared, r = 1 as can be seen here:

  a = (b *  q) + r
100 = (3 * 33) + 1
100 =      99  + 1

The above can be written In words as “100 divided by 3 is 33 with a remainder of 1”.

5

It appears it all depends on if you are refering to fractions or decimals. Or floating point numbers. Deppending on the situation either may be useful.

I will reflect on your answer and marios from a language perspective.

I cant see how tiddlywikis remainder is not also modulo.

The existing remainder is useful, as it would be if called modulo, the key value of modulo is it is ideal for converting between bases eg binary, decimal, hex etc… manipulating hours, minutes and seconds and more.

6

You really started something here, Tones. Can of worms, cat amongst the pigeons…

I’ll just throw this in here and leave – quickly…

              0!

7

Interesting, I did not know about Zero factorial.

  • Don’t get me started on Primes, especially the Prime factorial

I think this post says a few things about me;

  • I may occasionally have a brain fart
  • I am prepared to accept if I am wrong
  • Although I am prepared to question “authority” or the status Quo
  • I like exploring ideas
  • I am still not sure why this remainder looks like modulo and I often think of remainders as decimals, after you remove the integers.

Curious

8

The first section of the linked page: Modulo - Wikipedia states:

For example, the expression “5 mod 2” evaluates to 1, because 5 divided by 2 has a quotient of 2 and a remainder of 1

Also see the Remainder info at MDN (Mozilla Dev Network)

The wikipedia page also contains an overview, how different programming languages implement the modulo operation. Javascript seems to use an algorithm named “Truncated”

9

My avatar, the fine structure constant, is a beautiful thing. But the following, to my mind, makes the proposition that we’re experiencing a simulation a debatable possibility:

image
   Euler’s equation

Every time I come across it, and think about it… I get “lost”… seemingly for hours.

10

A mathematical remainder operator is almost identical to the modulo one, except for the sign of the value returned.

If n and m are positive integers, then there is no difference between the two, and n mod m is always in the set {0, 1, 2, ... (m - 1)}.

It’s common to call the C-style operator % “modulo”, but it’s usually not, because, as MDN makes clear, the sign of n % m is the sign of n (assuming that n and m are appropriate numbers.) It’s truly a remainder operator.

Thus -17 mod 4 is 3, but -17 % 4 is -1.

Coward! :slight_smile: You really need to stay and fight these things out. We both know there is a real answer, and we understand why it’s not what some people assume. So it’s incumbent upon us to correct them.

duty_calls

Yes, a thing of absolute beauty!

11

There’s safety in “numbers” :wink: