As @TW_Tones pointed out, there are plenty of ways to do loops. But you can also use recursion to solve such problems. Recursion is generally easy to use in TW. Your problem is too general, but I will demonstrate how to solve another one, which should give you some ideas.
Here we look at a mathematical recursion, calculating the Collatz sequence from a starting number.1 The Collatz Conjecture says that a sequence of integers, where the next one is found by following the following rule, always eventually reaches 1:
![]()
For instance, if we start with 3, it’s odd, so we multiply by three and add one, giving 10. This is even, so we divide by two, giving 5. This is odd, and 3 * 5 + 1 gives 16, then we keep dividing by two, giving 8, then 4, then 2, then 1.
3 → 10 → 5 → 16 → 8 → 4 → 2 → 1
As obscure as this problem sounds, it’s quite famous. Finding the sequence for a starting number is a good example of a recursive problem.
We can convert the math pretty easily to wikitext, especially with the introduction of the Conditional Shortcut Syntax. Here’s my version:
\procedure collatz(n)
<% if [<n>match[1]] %>
1
<% elseif [<n>remainder[2]match[1]] %>
<<n>> → <$transclude $variable="collatz" n = {{{ [<n>multiply[3]add[1]] }}}/>
<% else %>
<<n>> → <$transclude $variable="collatz" n = {{{ [<n>divide[2]] }}}/>
<% endif %>
\end
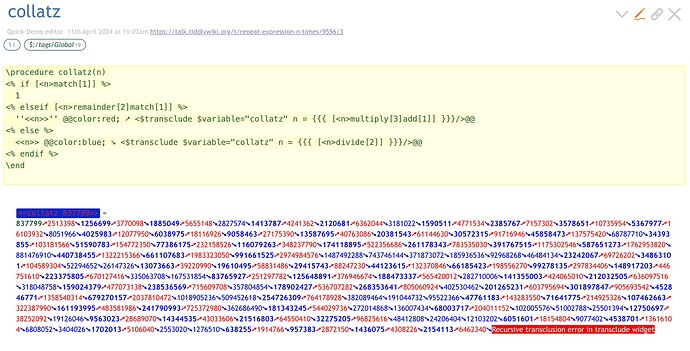
With this, <<collatz 3>> yields 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1, <collatz 1>> yields 1, and <<collatz 27>> yields a string of 111 integers, going as high as 9232 before eventually reaching 1.
We have a base case, when n is 1, and when it’s not, we recur on 3n + 1 if n is odd, and on n / 2 if n is even, recursively calling our collatz procedure on the resulting value.
collatz.json (524 Bytes)
1 So, I’m a math geek, so what?

 . But that’s another story.
. But that’s another story.