Problem with the Levenshtein operator?

Developers
#1

I’m putting this in the developer category because after trying to find what I was doing wrong, I think the problem is something deeper and too deep for me.

I was trying to use the Levenshtein operator on csv strings and getting results from computations that didn’t make sense. I think it is relevant that my strings are expected to be quite different at this stage except for the fact that being csv strings, they will have a few commas in them.

If I understand Levenshtein distance correctly, the largest possible distance between two strings is the number of characters in the longer of the strings. As I dug into why my calculations seemed off I found that I was sometimes getting Levenshtein distances that were greater than the length of the longer string.

I assumed I was just feeding the operator something other than intended since I was calculating my strings in filters but I have now tested filter defined strings, strings stored in fields, strings stored using \define and hard coded strings (e.g. [[cat]levenshtein[dog]] ). When the strings are completely different (like cat and dog) or very similar (cat and cot) the results are as expected but when the strings are very different except that they have a character or two in common in very different positions the distance returned can be greater than the length of the longer of the two strings.

For example [cat]levenshtein[dogc] returns 5 when it is really a 4 character operation to turn one into the other.

I made a little test tiddler than can show the effect of inserting a single a string (shows the problem best with a string consisting of a single character but longer strings work) into 2 strings that are completely different (I used upper and lower case versions of each other for clarity) and then calculating the distance and comparing it to the maximum possible distance (see https://levenshtein-test.tiddlyhost.com).

From looking at a lot of different versions of the table (different string lengths and insertion positions for the common string), it looks to me like the algorithm is making whatever additions or deletions are needed before the common section in order to make the common section of the two strings line up (so in the cat dogc example above, it makes 3 deletions from the beginning of dogc to line up the c in both strings, then 2 additions ( a and t) to the end of the string to get cat. That method works in many cases but in this case gives a distance of 5 but just deleting the c in dogc and replacing dog with cat is the better operation in this case and gives a distance of 4, which is the expected maximum.

Here is an example of the table showing a series of bad distances-

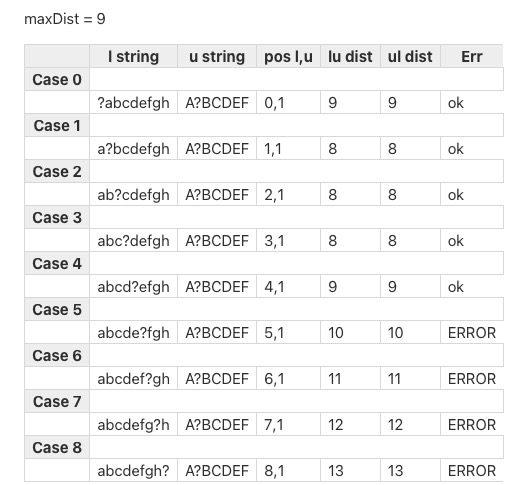
Screenshot 2024-11-23 at 14.01.23

Entries in the table marked ERROR are just the ones where the distance calculated exceeds the maximum distance. There may be cases when the calculated distance is less than the maximum but still greater than what it should be.

Unless I have misunderstood something about how this operator is supposed to work or I’m doing something silly, I think I have gotten as far as I can with understanding this.

Thanks for any feedback!

#2

Thank you @DBH, that is all very surprising. The Levenshtein operator comes from Google’s diff-match-patch library:

The docs there confirm that the maximum distance is the length of the longer string, and so it is particularly surprising to find we’re getting a different result.

The implementation is quite fiddly, but I think seems consistent with the behaviour we’re seeing:

The implementation of TiddlyWiki’s Levenshtein operator itself is here:

#3

That project has had no maintenance in years, and is now archived. I wonder if it’s time to switch to a well-maintained fork. I have no idea if that will address the main issue here, but it’s probably still a good idea.

#4

Could it just be its not suffcently parsing the csv format before doing comparisons? perhaps convert it to plain text without the quotes, commas etc…?

1 Like
#5

The implementation of the Levenshtein distance function appears to be the same in the fork.

Your demo is helpful, it might be interesting to also display the diff between the two strings so that it is easy to count through the changes.

#6

I tested, and the newer fork has no fix for this. But the main point was that if we fix the underlying issue, working with a maintained repo, we can submit our fix back to the project.

#7

And I just looked at the code. This is obviously not a real Levenshtein algorithm. It’s based around a tool that wants to consolidate the changes into longer strings. So it’s trying to find the Lev-distance between ?abcdefgh and ABCDEFGH? based on a diff object that looks like this:

  [
    { '0': 1, '1': 'ABCDEFGH' },
    { '0': 0, '1': '?' },
    { '0': -1, '1': 'abcdefgh' }
  ],

which is essentially:

INSERT 'ABCDEFGH'
KEEP   '?'
DELETE 'abcdefgh'

And then it simply adds together the lengths of the insert and delete strings to give a result. It doesn’t handle substitutions.

I think we need to find or create a better Levenshtein distance implementation.

#8

Hi @Scott_Sauyet I’m open to fixing/replacing the existing operator, but I do wonder whether we might not just document the peculiarities and leave it at that. The Levenshtein operator was something fun we got for free from the diff-match-patch library, and I don’t think would have made it into the core if it had existed as a separate library.

#9

That could make sense. As far as I can see, the only likely use of this operator in TiddlyWiki is to list the top fuzzy matches to a search string. This broken implementation should still be reasonable at ordering matches.

On the other hand, it would be nice to have this correct. And it’s quite trivial to write our own. I wrote an obviously correct one-liner yesterday. Then I woke myself up in the middle of the night night designing an actually efficient algorithm. I just checked, and it’s the same one Wikipedia recommends. At some point today or tomorrow, when I’m in front of my computer, I’ll test it out, and we can see if we want to update.

3 Likes
#10

Great! FYI the Levenshtein (properly done) would be useful to me.
Maybe I’m an edge case but it is v. useful as an adjunct to string query and analysis.
Outside TW I often use it alongside Regex.

Just a comment, TT

#11

First, thanks for taking a look at this. Glad in a way that I was right about the problem but do wish it had been something trivial.

I just wanted to add that it is a specialized fuzzy search that I’m working on. I was trying to normalize to get a match quality between 0 and 1 and then put a quality cut on the possible matches. Fine tuning it and some other details made it a bit more complicated than just doing some subtraction and divisions with the min and max distances but that is the general idea. Getting levenshtein distances out of range threw my final values off enough to be very noticeable. (For now I’ve added a min operator to take the minimum of the Levenshtein operator result and the max distance before I try to use the distance, but not sure that there aren’t edge cases where the reported distance is less than the maximum but still wrong.)

#12

Interesting!

I am no TW programmer but I do see clearly TW is a great vehicle to iteratively develop v. precise applications.

That maybe marks it off from the general swamp of variations that lack clarity of aims.

Your explanandum of aims is very interesting and, I hope, understood.

TT

#13

Without much additional comment, here are the two implementations.

First, the elegant and clearly correct, but inefficient, recursive version:

const lev = (x = '', y = '', a = x[0], as = x.slice(1), b = y[0], bs = y.slice(1)) => 
  !b 
    ? x.length 
  : !a 
    ? y.length 
  : a == b ? 
    lev(as, bs)
  : 1 + Math.min (lev(x, bs), lev(y, as), lev(as, bs))

lev('kitten', 'sitting') //=> 3
lev('Saturday', 'Sunday') //=> 3
lev('a?bcdefgh', 'ABCDEFGH?') //==> 9

Second, a more efficient, but harder to understand, bottom-up dynamic programming one:

const lev = (x, y) => {
  let j = 0, 
      row = Array.from({length: x.length + 1}, (_, i) => i)
  while (j < y.length) {
    row = row.reduce((a, c, i) => {
      const s = y[j]
      const t = (i == 0) ? '' : x[i - 1]
      return a.concat(i == 0 ? c + 1 : Math.min(
        (s == t ? row[i - 1] : row[i - 1] + 1), 
        a[i - 1] + 1, 
        row[i] + 1
      ))
    }, [])
    j += 1
  }
  return row.at(-1)
}

lev('kitten', 'sitting') //=> 3
lev('Saturday', 'Sunday') //=> 3
lev('a?bcdefgh', 'ABCDEFGH?') //==> 9

With all the index twiddling and the mutation, that latter would need more substantial testing to make sure there are no corner cases.

Either of them would still need to be rewritten in TW house style, but that’s mechanical.

In fact, if we do decide to replace our Levenshtein function, I would suggest our first stop would be a better-tested publicly available version, so long as the code is reasonably short.

Hearing the OP’s reason for noting this, I am in favor of replacing this function, one way or another. It could well bite others with similar needs. I doubt anyone is wedded to the broken behavior, but if we wanted to keep it available, we could expose it under a different name.

3 Likes
#14

It would be nice if we could do this with some changes or introduce a mechanism. An example may be a plugin that allows either the new behaviour, or the old behaviour depending on what is implemented.

1 Like
#15

I think this needs to be fixed upstream. The upstream JS repo seems to have some tests, but they do not catch the problem. … I’ll have a closer look.

1 Like
#16

If so, then we’d need to switch to a fork, since the original repo is archived. Perhaps the fork I mentioned above.

But given the design of the current upstream implementation, it would probably involve a total rewrite there too.